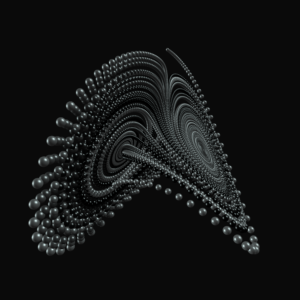
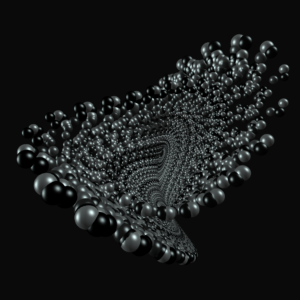
Hashtractors

Hashtractors are a collection of generative renderings of various parametric equations commonly know as “strange attractors”. These equations are at the heart of chaos theory; a branch of mathematics focused on the study of dynamical systems that are highly sensitive to initial conditions. A selection of 30 different equations has been made for this collection. Hash data is used as their parameters.

(a) 0: Aizawa

(b) 78: Lorenz

Motivation

I have been fascinated with chaos theory since I first read Chaos, by James Gleick in my teenage years. Back then I did not know how to program, but the beauty and intricacy of images and the plottings in the book were so engaging, that they made a deep impression on me, philosophically speaking.

The first time I used a chaotic system for creative purposes was around 2013 while doing some audio experiments in the SuperCollider programming language, during my studies. These are wonderful sources of entropy as modulators for oscillators, given that their behavior is volatile yet rewardingly cyclical if given the correct parameters.

In 2017, I created a live audiovisual performance titled Strange Attractors, where I aimed at exploring the properties of the equations more deeply via various methods. For this project, I did extensive research and ended up with a small library of sorts to sonify and visualize them via diverse techniques.

I have revisited this collection of equations in one way or another over the years, both in the audio and visual domains. I find that they create structures that are both beautiful and mysterious.

(a) 05: Sakarya

(b) 102: Rayleigh-Benard

Concept

When the opportunity to present something in Artblocks came in, I wanted my very first project to be something of manageable size, collectible, and that felt home, so I went ahead and once more dug into my library to repurpose these chaotic equations. The name for the project was the first thing I had since I could not resist the wordplay of “hash” and “strange attractor”, hence “Hashtractors”.

Aesthetics

In choosing the aesthetics for the piece, I looked for something that I considered visually very different than what I had mostly seen on the Artblocks platform, which was at the time full of color and overwhelmingly 2D. I decided to go against the current and do something purely monochrome, rendered in 3D. These constraints set up the tone for the final look of the project and guided the overall implementation.

Creative process

If there is something to know about these equations is that they are extremely sensitive to initial conditions. This property prompted Edward Lorenz to seriously analyze the discrepancies he saw in his limited models for weather prediction back in the ’60s. It did not seem rational that such wildly different results could come out of rounding errors in the numerical outputs of the computers alone, so he devoted himself to find out what was the cause for the unpredictable results he was getting. He had programmed the very first documented “strange attractor”. His research prompted the study of chaos and founded a new science to study complex phenomena. It turns out that the world is full of unpredictable behavior, governed by underlying patterns of intricate dynamics too convoluted to account for.

As a primer on this fascinating topic, I recommend reading this article in “how stuff works”.

(a) 24: Thomas

(b) 68: Nosé-Hoover

But what does it mean in practice that these systems are “extremely sensitive” to initial conditions”? It means that for any given input, even the tiniest difference can result in a completely different (and possibly unwanted) output and that it is ultimately impossible to predict what certain inputs will do. One can imagine that preparing generative on-chain artwork with input that is virtually random can be challenging.

Indeed, the task that took me the longest in preparing the artwork was finding a broad enough set of good value combinations that could provide variety and remain visually engaging. No input works for two equations, so I had to devise a scheme to remap ranges per attractor. I go into detail on this scheme in the technical section of this article.

In some cases, the equations were so hard to control that I had to settle for hard-coded values and allow for variation elsewhere (rotation along some axis, for example). In others, I discarded the attractor altogether, since it was not predictable enough to warrant a satisfactory mint. I reduced the number of possible shapes one can get from an initial of about 40 to only 30, and spent a considerable measure of time running scripts and generating output to ensure that none of the systems “exploded”.

(a) 77: Hadley

(b) 108: Qi-Chen

Distribution model

The distribution model I had in mind was that some collectors could create a “full” set of all available equations. A complete set would contain all the 30 different equation systems. I initially planned to potentially allow for at least ten such collections, which would mean 300 mints at minimum. However, after testing the “mint resistance” of the algorithm, as in how many mints it could support until producing too similar results, I estimated that the optimal mint size would be at around 128. That reduced the possibility of collections to about four, but I was at least sure that the whole would be the best it could be, visually speaking, which is by far more important.

In practice, given the uniform random distribution that the algorithm uses for type selection, the actual number of available collections would be more between one and three. Since the final minted collection online has an instance of one of a kind attractor type (Rucklidge), there is in fact only one possible “full” collection that could be formed by an eager collector.

(a) 96: Rucklidge (the rarest Hashtractor)

(b) 16: Three scroll unified

If you are curious about the statistics of the whole collection, you can check this guide by Rev Dan Catt, with a list of features and other engaging information.

Scarcity

For this project, there was no engineered “scarcity”, in the sense that I did not deliberately introduce “rare features” of any kind. The reason for this is twofold. Given the low number of mints, some attractor types would be rare enough already, with 2 to 4 average occurrences. On the other hand, I could not think of any feature for which the use of probabilistic manipulation would be justified. I like each one of these shapes too much to arbitrarily condition one or another to existence! The fact that there’s only one Rucklidge attractor in the whole collection is pure chance. The only scarcity that was planned is, as aforementioned, a full Hashtractor collection (go hunt!).

Technique

The technique employed is very simple. Given a set of non-linear equations as functions of time, for example for the Lorenz attractor in figure 1.b, where constants $ sigma = 10.0 rho = 28.0 $ and $beta = 8/3$ :

begin{align*}
frac{dx}{dt} = sigma * (y – x) &&
frac{dy}{dt} = x * (rho – z) – y &&
frac{dz}{dt} = xy – beta z
end{align*}

One has to simply update dimensions (x), (y), (z) over some number of points (n) and variable time (t), such that:

begin{align*}
x_{n} = x_{n-1} + (x_{n-1} * t) \
y_{n} = y_{n-1} + (y_{n-1} * t) \
z_{n} = z_{n-1} + (z_{n-1} * t)
end{align*}

In Hashtractors, for any attractor type, a total of 10000 points are sampled. These are pre-computed in an array before rendering. There is no draw loop in the code since the output is not animated and therefore needs to be computed only once. Essentially, the code to compute any given attractor would be something like this (in Javascript), where the function update() is defined as above and returns a 3-dimensional point:

let points = [];
for(int i = 0; i < n; i++) {
   let point = update();
   points[i] = point;
}

The center of a sphere corresponds to each of these points. Each sphere’s dimension is relative to its distance towards the center of the attractor. Since the equations give values on different ranges, all coordinates had to be normalized, in the range (-1, 1) to ensure proper rendering within the limits of the canvas.

I chose to use spheres to represent points and not drawing a continuous line or mesh because then the differences between input values would be more noticeable.

Challenges

As mentioned before, the major challenge was to come up with good values for the inputs of each attractor type. The scheme I ended up using was to arrange data that describes either fixed values or ranges for a given input, here for example the parameters used for a Lorenz attractor:

 

let time = map(nt, 0.0, 1.0, 0.009, 0.02);
let rotation = [ 0.0, 0.25, 0.45, 0.55, 0.75, 0.1, 
      0.25, 0.5, 0.75, 0.75, 0.6, 0.8]; 
let scale = [ 1.0, 1.1, 1.2, 1.25, 1.1, 1.0, 
      1.15, 1.3, 1.1, 0.95, 0.9, 0.9];
let angle = [ 'y', 'y', 'y', 'y', 'y', 'x', 
      'x', 'x', 'x', 'xy', 'xz', 'xz'];
let orientation = [ [0.0, 0.0, 0.0], [0.0, 0.3, -0.1], [0.0, 0.1, 0.0], 
      [0.0, 0.0, 0.0], [0.0, -0.2, -0.2], [-0.2, 0.0, 0.0],
      [-0.25, 0.0, 0.0], [0.0, 0.0, 0.0], [0.2, 0.0, 0.0],
      [0.2, -0.4, -0.1], [0.4, -0.3, -0.1],  [0.0, 0.0, 0.0]
   ];

Each of these parameters gets selected using the uniform distribution from the hash, as 8-bit numbers in the range 0-255. These seeds are used as indices, wrapping around the length of the array of values of the given parameter. You can see that in this pseudo-code below, in the operation for type selection. The other parameters follow a similar logic.

// type, time, rotation, scale, angle and orientation
let type = sum(seeds) % attractors.length;
selectType(type, seeds[0], seeds[1], seeds[2], seeds[3], seeds[4]);

Conclusions

I was extremely surprised by the reception of the project, which could not be more enthusiastic. The speed and the general feeling around an NFT drop in this platform are surreal. Hashtractors sold out in 1 minute and 35 seconds (according to info from rarity.guide), with an average of more than 1 per second, which sounds to me like madness. It can be due to a small army of bots operating in the dark, considerable eagerness for the project, or a combination of both. Either way, I am still thinking and coming to terms with the dynamics of this novel market, and what it entails for generative artists and collectors in a broad sense, both the good and the bad.

List of systems

Here are all the systems used in this project, for those wishing to implement strange attractors. You can find the equations in the PDF version of this article below.

1. Act
2. Aizawa
3. Arneodo
4. Burke-Shaw
5. Chen-Celikovsky
6. Chen-Lee
7. Coullet
8. Dadras
9. Dequan-Li
10. Finance
11. Four wings
12. Hadley
13. Halvorsen
14. Lorenz

15. Lorenz mod 1
16. Lorenz mod 2
17. Lu-Chen
18. Newton-Leipnik
19. Nosé-Hoover
20. Qi-Chen
21. Rayleigh-Benard
22. Rucklidge
23. Sakarya
24. Shimizu-Morioka
25. Thomas
26. Three scroll unified 1
27. Three scroll unified 2
28. Wang-Sun
29. Wimol-Banlue
30. Yu Wang

Acknowledgements

I want to express my gratitude to the Artblocks team, the collectors, and the community in general, whose focus and appreciation of generative art are unbelievable and inspiring.

I propose a toast for all the scientists and researchers that discovered these beautiful systems of equations. Cheers! 🍺

PDF version

Get PDF

Links and additional information

• Beautiful work with Strange Attractors by Chaotic Athmospheres.
•  A nice primer about chaos and fractals, from the Space Telescope Science Institute.
• Chaos: Making a New Science,  a classic by James Gleick.
• Complexity: A Guided Tour, by Melanie Mitchell.